Netty 是怎么做内存管理--PoolChunk

Netty 是怎么做内存管理–PoolChunk部分。

Preface

我们将PoolChunk上的内存分配视为一个算法来分析：

• 输入：指定的连续内存空间大小
• 输出：如果分配成功，返回一个包含目标空闲内存地址信息的句柄，否则返回失败

这里强调以下，Netty内存池分配出来的内存空间不是Client申请size的大小，而是大于size的最小2的幂次方（size > 512）或者是16的倍数。比如Client申请100byte的内存，那么返回的将是128byte。Netty会在入口处对申请的大小统一做规整化的处理，来保证分配出来的内存都是2的幂次方，这样做有两点好处：内存保持对齐，不会有很零散的内存碎片，这点和操作系统的内存管理类似；其次可以基于2的幂次方在二进制上的特性，大量运用位运算提升效率。后面的详细流程中我们将会看到。

内存存储单元

在分析原理之前，我们先看以下PoolChunk中一些默认参数：

1.内存块Chunk，Netty向操作系统申请资源的最小单位，chunk是page单元的集合

• chunk默认大小16M，可调节，根据pageSize和maxOrder计算得到

• MaxChunkSize, chunk最大大小为1G

• DefaultMaxOrder = 11, 一个chunk默认由2¹¹个页面构成，因为一个page 8k，所以默认完全二叉树11层。

2.内存页Page，当请求的内存小于页大小时，可继续划分为更小的内存段，使用位图标记各使用情况
Page大小的默认值为8K,可调节，必须为2的幂：

Data structure

Chunk基于一个完全平衡的二叉树来管理它拥有的Pages，每个叶子节点表示一个Page。参考前述的默认参数：
ChunkSize = pageSize*2^maxOrder, 也就是Page的个数是2的幂次方个，那么以此为叶子节点的二叉树一定是完全平衡的二叉树。二叉树中的父节点包含所有子节点的内存，也就是说父节点可以使用和分配以其为根的所有子节点表示的内存空间。其在内存分配的过程中（Page级别的分配），总是在此二叉树上（从左到右）寻找最先最小满足条件的Pages。

表示方式

Netty使用了一个数组memoryMap来表示这个完全二叉树，数组元素的语义与二叉树拓扑结构的对应关系如下图: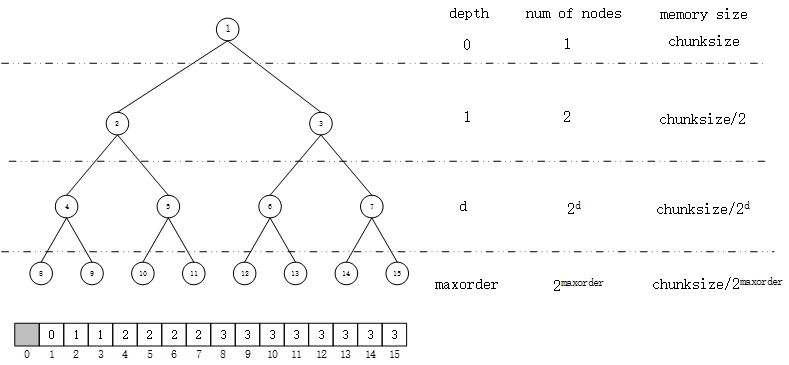

详细的来说，数组下标表示二叉树中各节点的编号id，数组元素内容表示当前节点可分配内存的子节点（即未分配）在二叉树中的深度。根据i节点在memoryMap中的取值不同，它可以有一下三种语义：

1. memoryMap[i] = depth_of_i 当前节点及其所有子节点都可以用来分配
2. memoryMap[i] = x > depth_of_i 至少有一个子节点被分配，无法直接使用此节点，但其在第x层的子节点中有可分配的内存
3. memoryMap[i] = maxOrder + 1 当前节点的所有子节点均已被分配

以上图节点3为例，当memoryMap[3]=1时，表示该节点及其子节点均可分配，memoryMap[3]=2时，表示节点6和7中至少有一个已经被分配，并且在这两个节点中还能找到未分配的空间，memoryMap[3]=4时，表示该节点下的所有空间均已经被分配，无法再使用。

Procedure

先看代码：

1
2
3
4
5
6
7
8
9
10

/**
 * 向PoolChunk申请一段内存
 * /
long allocate(int normCapacity) {
    if ((normCapacity & subpageOverflowMask) != 0) { // >= pageSize
        return allocateRun(normCapacity); // 当要分配的内存大于pageSize时候，使用allocateRun在chunk内分配
    } else {
        return allocateSubpage(normCapacity); //否则使用向PoolChunk申请一段内存在page内分配
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

/**
 * Allocate a run of pages (>=1)
 *
 * @param normCapacity normalized capacity
 * @return index in memoryMap
 */
private long allocateRun(int normCapacity) {
    int d = maxOrder - (log2(normCapacity) - pageShifts);
    int id = allocateNode(d);
    if (id < 0) {
        return id;
    }
    freeBytes -= runLength(id);
    return id;
}

首先根据请求内存的大小，选择采取合适的分配策略，这里详细讨论分配大于一个页面大小的情况，页内分配请移步Netty 是怎么做内存管理-PoolSubpage

再根据请求内存的大小，定位其在二叉树中的深度：int d = maxOrder - (log2(normCapacity) - pageShifts)。参考前述二叉树的图，可以有两种理解方式：

1. 自底向上：父节点的内存是子节点的二倍，比子节点高一层；父节点的内存是孙子节点的四倍，比孙子节点高两层，所以拥有normalCapacity内存的节点应该比叶子节点高：log2(normalCapacity/pagesie) = log2(normalCapacity)-pageShifts层，也就是说它在树中的深度应该为maxOrder-(log2(normalCapacity)-pageShifts).
2. 自顶向下：观察上图右侧说明信息的第三列，根节点拥有整个chunk的内存，任意d层节点拥有的内存Capacity=chunksize／2^d, 两边取对数可得拥有normalCapacity内存的节点应该在log2(chunksize/normalCapacity)这一层上。

下面看最核心的一段：如何利用memoryMap在d层上寻找第一个可用内存节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

/**
 * Algorithm to allocate an index in memoryMap when we query for a free node
 * at depth d
 *
 * @param d depth
 * @return index in memoryMap
 */
private int allocateNode(int d) {
    int id = 1; // 从根节点开始计算
    int initial = - (1 << d); // has last d bits = 0 and rest all = 1
    byte val = value(id);
    if (val > d) { // 根节点的容量不足以满足要分配的内存大小
        return -1;
    }
    while (val < d || (id & initial) == 0) { // id & initial == 1 << d for all ids at depth d, for < d it is 0
        id <<= 1; //取左子节点
        val = value(id);
        if (val > d) {
            id ^= 1; //取邻居节点（2->3, 3->2）
            val = value(id);
        }
    }
    byte value = value(id);
    assert value == d && (id & initial) == 1 << d : String.format("val = %d, id & initial = %d, d = %d",
            value, id & initial, d);
    setValue(id, unusable); // mark as unusable
    updateParentsAlloc(id);
    return id;
}

1
2
3

private byte value(int id) {
    return memoryMap[id];
}

这一段的核心思想是：

从根节点开始，如果根节点已经被分配，并且其可分配内存的子节点深度大于d，表示已没有足够且连续的内存空间用来分配，返回-1；

如果左子节点上的内存可分配则在左子节点上分配，否则尝试右子节点，依次迭代。

这里主要注意下循环的迭代条件：

1. 如果当前节点可分配节点的深度小于目标深度（相应的内存也就大于请求的内存），说明子节点就能够满足条件，进入下一层；
2. 当一个节点(id)可分配节点的深度与目标深度相等时，只要当前节点(id)的深度小于目标深度（id & initial == 0），就应该进入下一层迭代到目标深度那一层，寻找可用的节点。

更直观的来看，如下图:

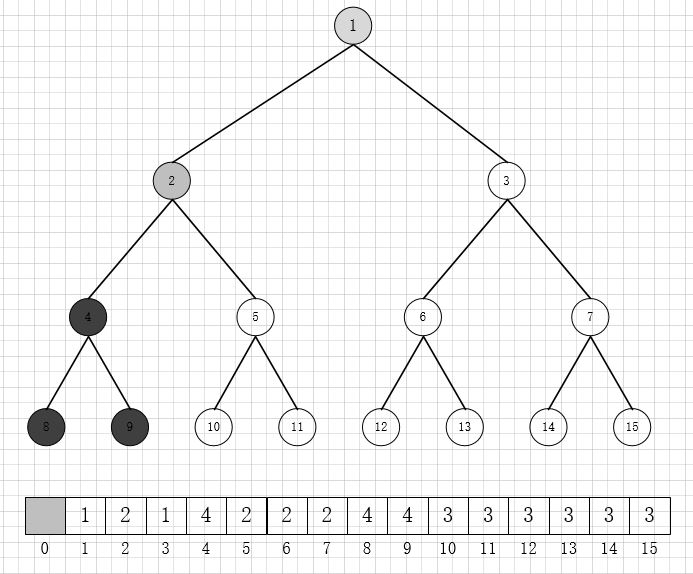
假设现在经过内存的分配，我们待分配的内存应该在第二层d=2上寻找，首先从根节点1开始，memoryMap[1]=1 < d，符合迭代条件1，进入左子节点2；

memoryMap[2]=2=d，说明节点2在第二层的子节点上有内存可以分配，虽然此时已不满足迭代条件1，但节点2的深度还是要小于d的，满足迭代条件2，进入左子节点4，由于4的叶子节点都被分配，已经被标记为不可用（val = maxorder+1），所以尝试邻居节点5;

由于memoryMap[5]=2 并且 5 & initial != 0, 无法再迭代，推出循环，找到目标节点5.

分配完成后需要将当前节点标记为不可用，并更改将父节点可分配节点的情况，防止重复分配。具体的步骤如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

/**
 * Update method used by allocate
 * This is triggered only when a successor is allocated and all its predecessors
 * need to update their state
 * The minimal depth at which subtree rooted at id has some free space
 *
 * @param id id
 */
private void updateParentsAlloc(int id) {
    while (id > 1) {
        int parentId = id >>> 1;
        byte val1 = value(id);
        byte val2 = value(id ^ 1);
        byte val = val1 < val2 ? val1 : val2;
        setValue(parentId, val);
        id = parentId;
    }
}

过程比较简单：从当前节点开始向上回溯，以当前两个子节点memoryMap中取值较小的那个，来更新父节点的值，这样就维持了节点memoryMap[id]的语义：在第x层的子节点中有可分配的内存。